Quantum Computing Applications for the Energy Industry
Many have probably heard of quantum computing, including a lot of recent news about its promised ability to compute solutions to problems currently unachievable by even the largest supercomputer built to date. In fact, no computer using the classical concept of a single bit representing either a 0 or a 1, could even theoretically be built to compute exact solutions to many problems called NP-Hard, which are known to scale exponentially—there are not enough atoms in the universe to even represent every possible combination.
However, a couple decades ago physicist Richard Feynman theorized a new kind of computing device built using the concepts of quantum mechanics that could one day be used to take on these difficult problems. He was thinking primarily of simulating the behavior of quantum systems likes subatomic particles and molecules but since his initial idea, many others have realized the application to other problems that scale exponentially and even ones that scale in polynomial time and could be improved to scale in logarithmic time.
To build a quantum computer you must harness the quantum nature of fundamental particles like electrons, ions, and photons and manipulate and measure their quantum states of spin and polarization respectively, so they may represent a bit, called a qubit, for the purposes of computation.
Take for example the quantum spin of an electron. An electron’s spin along any axis may be observed as either up or down representing a 0 or a 1, but in quantum mechanics, an electron’s spin may also be in a superposition of both, expressed as a linear combination of two states at the same time. This is one advantage of the qubit. When in superposition a single qubit represents two states and when combined with n qubits represents 2n states. Now, we can never observe a quantum system in a superposition state, but we may manipulate the probability of the linear combination so that when we do observe it, we have a great chance of seeing a result that represents the solution to the problem we seek. The second advantage of the qubit is that two or more can be entangled so that when observed, the outcome of one qubit also determines the outcome of the entangled pair, even when in a superposition state and even if placed on the other side of the universe. Albert Einstein called this “spooky action at a distance”.
That’s it, these two basic concepts yield a powerful computing device where n qubits operate in a 2n space and can be used to solve many problems that scale exponentially. It is important to point out that a quantum computer can function exactly as a classical computer, with qubits representing 0 or 1, but is more general in its added capability of superposition and entanglement. To use this added capability however we are faced with a completely new way of thinking of algorithms and writing software. The change will come slowly but the advantages will be dramatic.

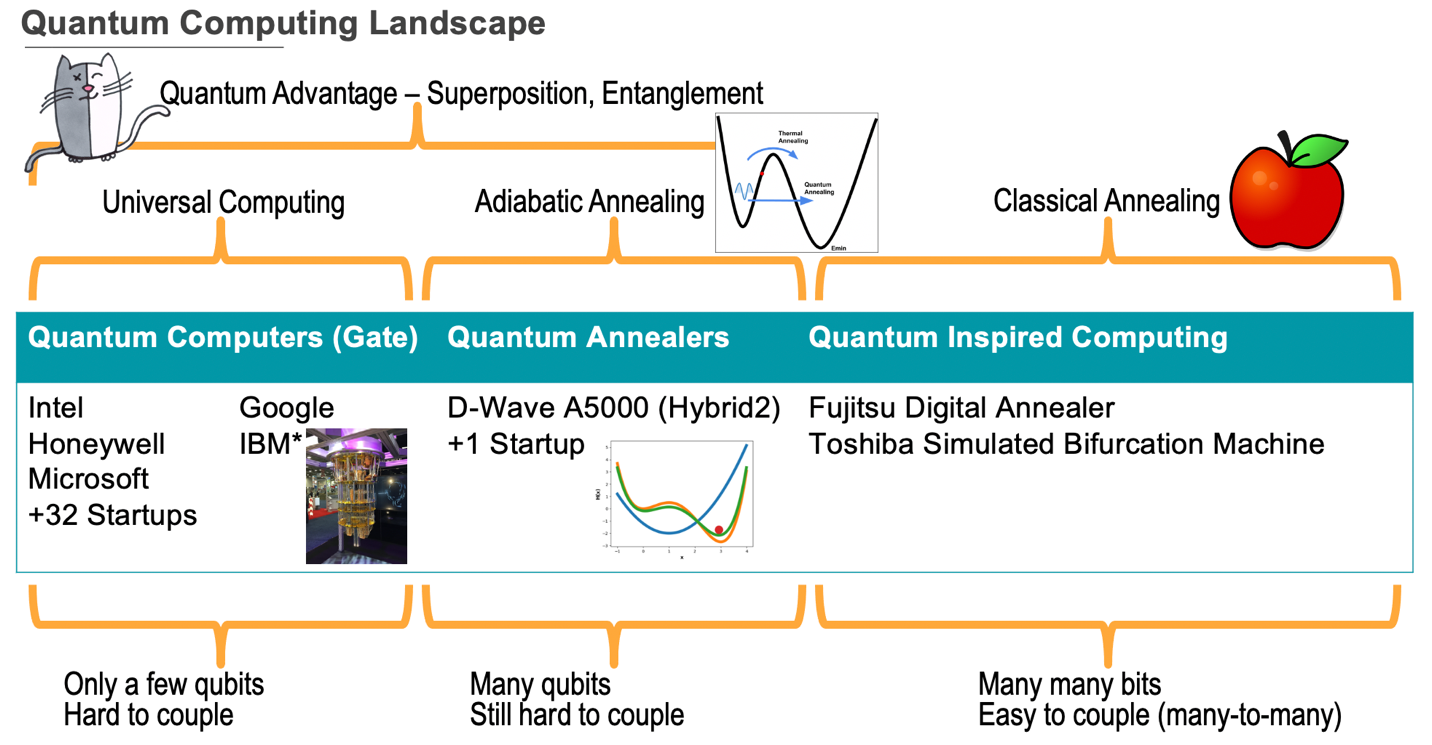
Many large technology companies like IBM, Google and Honeywell have started building quantum computers and are solving the difficult engineering problems associated with controlling and isolating single electrons, ions, or photons and scaling the number of these to tens, hundreds, thousands and even millions needed to solve many problems. Smaller startup companies are also looking to be the first to develop novel hardware and software stacks that deliver enough of a competitive edge to lead this new industry, including D-Wave Systems, Rigetti and Ion Q. In the case of D-Wave Systems, they chose to develop hardware called a Quantum Annealer that specifically solves combinatorial optimization problems, whereas the others are building universal computers based on fundamental gate operations similar to the function of the NAND gate in classical computers. The D-Wave Systems Quantum Annealer has the advantage of dedicating many more qubits—5,000 in the latest Pegasus processor—to solving problems, whereas the largest IBM quantum processor called Hummingbird comprises 65 qubits, but with a strategic roadmap to expand to over a thousand qubits in the next few years. It still is unclear which technology will prove the most effective, but the race is on and is heating up with more companies devoting significant resources towards this new computing frontier.

I’ve said a lot about what quantum computing is, but have not yet described many problems that it can solve. Many in the quantum computing industry feel that the original idea of simulating molecules and materials is the first best application of this technology. This is because simulations of intrinsically quantum systems like a molecule naturally align with the capabilities of quantum computers.
Early successes have been reported by companies like Mitsubishi who are using quantum computers to aid in the design of battery technology. Advanced chemicals and materials are also extremely important to the energy industry and range from a better understanding of the properties of hydrocarbons to chemicals used in oil and gas production, transportation and processing. Finding solutions to corrosion and solid formations that impact flow assurance could improve safety and reduce costs in our industry substantially. The development of solutions to these problems requires high precision simulations of molecules and reaction processes that would otherwise take years to explore experimentally. The next important application of quantum computers is in planning, logistics, and decision making.
One of the early successes in quantum computing and annealing have been in solving combinatorial optimization problems and some have claimed evidence of a quantum advantage over the best classical hardware and algorithms. These claims however have only resulted in even greater interest and renewed innovation. Nobody likes to lose, and authors of classical algorithms have learned what problem specific patterns are being exploited by quantum technology and have revised algorithms to yet again top the performance and robustness results. These revised or specialized algorithms have been called quantum inspired computing or optimization (QIO) and yield new technology offerings like Fujitsu’s Digital Annealing Unit and Toshiba’s Simulated Bifurcation Machine. The advantage these hardware and software have is the ability to deliver many bits using current classical electronic hardware such as GPUs and FPGA.
Combinatorial optimization applies to problems whose decision space is discrete and finite and commonly found in investing, planning, and logistics but also in machine learning and computer graphics. They are generally considered NP-hard problems to solve because the solution space scales exponentially with the number of discrete alternatives making computation of all alternatives intractable. First, I’ll describe a simple abstract example, often used to demonstrate quantum technology, that partitions a graph into two sets, such that the number of edges that span the two sets is maximized.
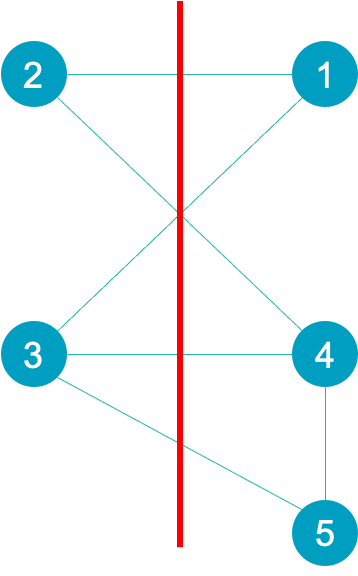
This is commonly called the Max-cut problem. Here we must decide in which set to place each node and count when an edge is cut. This problem can be represented as a binary combinatorial optimization problem by assigning a single qubit to represent each node whose value is 0 if in one set and 1 if in the other. A cleverly constructed function that counts the number of edges cut is used to determine the solution with the maximum cuts. This problem is NP-hard as the number of node assignment combinations is 2n which for large n is impossible to compute.
Although the max-cut problem is simple, albeit difficult to solve, industrial examples abound and are not limited to graphs, but tangible concepts like investments, resources, wells, and equipment. Decision making is critical to our industry due to the significant costs, safety implications, and high uncertainty, which demands the most complete evaluation of decision alternatives that time, and budget, can afford. I’ll give some examples of problems we are using quantum technology to help solve.
The first example relates to investment decisions whether whole assets, workovers, or infrastructure. Often the decisions may be binary and include planning aspects of time to invest. These decisions may include complex dependencies like budgets, resource availability or contractual obligations. We may seek to maximize the value derived by the decisions or minimize the risks incurred or somewhere in between.
Another example is related to planning of events. NASA is using quantum computing to best schedule a set of tasks performed by planetary explorers. These tasks require battery power, and scheduling too many high-power tasks too closely together can result in battery exhaustion or damage to the instruments, even when continuously charging during daylight hours. Carefully scheduled tasks are desired to fulfill mission goals and maximize battery levels.

In our domain we may consider the difficult problem of deciding where to place wells in a discretized field in a sequence demanded by the availability of drilling equipment. The choice of sequence may consider the expected cumulative value at each location, the costs of moving equipment to each new location and the impact of placing too many wells close together. Such problems are variations of the so called “Travelling Salesman” which attempts to find the sequence of locations visited by a salesperson that minimizes the total travel time. Such problems scale as n factorial which again for large n is intractable to compute all combinations.
Another example is in the field of unsupervised machine learning. Clustering is a common exploratory data analysis technique that seeks to partition data points into subgroups based on their similarity, generally determined by the Euclidean distance between points in m dimensional space. Data points in the same subgroup or cluster are nearby and therefore more alike than points that are further away and possibly members of other clusters. Such a clustering may define a classification of types and aid in the development of targeted models to predict future outcomes within each subgroup. The partitioning of n data points into k clusters is NP-hard to compute, as the number of partitioning combinations is kn and therefore grows exponentially with n.
Algorithms such as k-means have been developed that apply computational heuristics to seek the partitioning with minimum cumulative intra-cluster distances between data points. Often these heuristic based algorithms find local minimum solutions that may miss subtle and important similarities that could improve classification and accuracy of subsequent model predictions.
Chemistry simulation and combinatorial optimization problems are considered early opportunities for quantum computing because they are less sensitive to the impact of noise that is still a problem for current quantum computing hardware. The random flipping of a single qubit is unlikely to have a large impact to the final result of these problems. These class of problems are considered suitable for the noisy intermediate scale quantum (NISQ) devices of today. Future quantum computers that are more noise free, error corrected and comprising thousands or even millions of qubits can begin to be applied to other problems in our field, like unordered data searches, function inversion including large linear systems, and large integer factorization (the foundation of modern internet security). I mention these only at the end as no quantum computer exists that is even close to solving these problems and I prefer to avoid untoward hype that may mislead or misdirect what should be the application of quantum computing in our industry in the present or near future.
Author information: Rodney Lessard is a principal computational scientist located at the Schlumberger Software Technology Innovation Center in Menlo Park, CA USA. He received his PhD in physics in 1997 from University College Dublin in Ireland where he studied very high energy gamma-ray astrophysics using ground-based atmospheric Cherenkov telescopes pioneered at the Harvard-Smithsonian Astrophysical Observatory in Southern Arizona. He joined Schlumberger in 2001 as a senior software developer at the Calgary Technology Center located in Alberta, Canada and in 2010 transferred to Houston TX, where he was the technical lead of the multiphase flow network simulation engine in PIPESIM. In 2018, he joined the high performance computing team at STIC where he now innovates with emerging technologies like quantum computing and its application to the energy industry.

